In 1919, Arthur S. Eddington, Frank W. Dyson, and Mr. C. Davidson famously led an expedition to photograph a total solar eclipse and confirm Einstein’s prediction that massive bodies like the Sun could bend starlight. That photographic evidence became one of the first major tests of General Relativity. Here, using a digital remaster of the image, I’ll attempt to recreate the experiment measurements.

Tools and Data

These are the things needed to get going:

• A high-quality digitized image of the 1919 eclipse from ESO (link). This version uses image processing techniques to improve the image quality from the original photo plates.
• A sky map from Stellarium, set to the same region of sky but offset by 6 months to avoid the Sun’s interference.
• Affinity Photo for image overlay and alignment.
• Manual centroiding and pixel measurements to detect deflection.

Image Alignment

To ensure accuracy, I anchored both images using two distant reference stars — HR 1375 and 69 Tauri that are far enough from the eclipsed Sun to remain unaffected by gravitational lensing.

I loaded the original eclipse image as the background layer in Affinity Photo and locked it in place. Then I added the Stellarium-generated star field as a transparent overlay on top. By adjusting the opacity, I was able to see both sets of stars simultaneously for alignment. Notably, the star images from Stellarium appear significantly larger than the more compact and sharper ESO eclipse stars. In the cutouts shown in Figure 1, you can clearly see the difference. Each Stellarium star forms a large diffuse blob and the ESO image has its star as a bright point at the center.

After carefully stretching, rotating, and nudging the top layer, I aligned the two images so that the reference stars matched. It took a fair bit of trial and error, but I eventually achieved alignment within ±0.5 pixel, which is pretty decent for a manual process. This gave me confidence that any measured offsets for stars near the Sun were not due to alignment error — a point further supported by the zoomed-in cutouts shown in Figure 1, where the distant stars remain well-aligned.

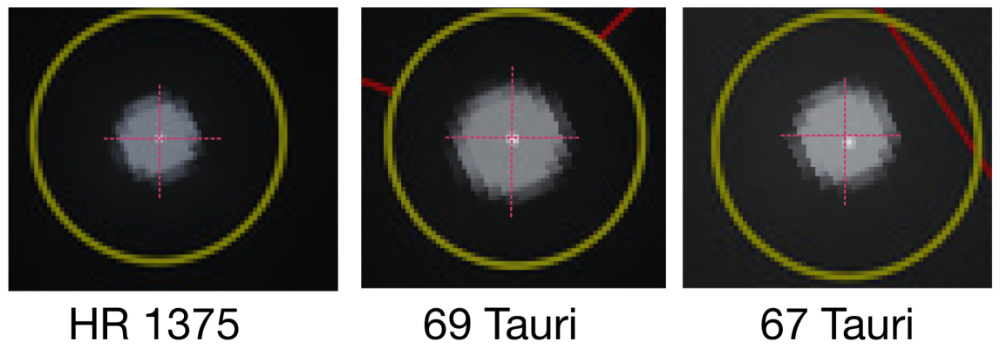
Here’s the annotated overlay, with 67 Tauri circled, and a zoomed inset revealing a small but visible offset between the eclipse photo and the reference sky:

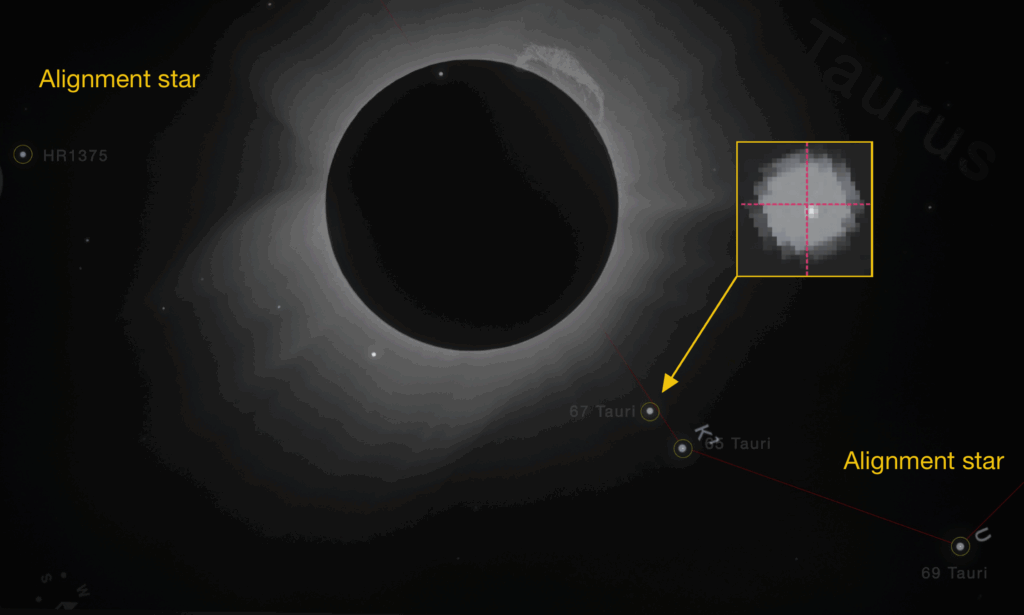
Measuring the Deflection

The distance between 65 Tauri and 67 Tauri in the eclipse photo was measured as:

• 160 pixels
• Calculated angular separation: 340 arcseconds

This gives a plate scale of

Scale = 340 arcsec / 160 pixels ≈ 2.125 arcsec/pixel

Zooming in on 67 Tauri, the observed centroid deflection between the reference and eclipse position is down and right and approximately:

1 pixels × 2.125 arcsec/pixel ≈ 2.1 arcseconds

Comparison to Einstein’s Prediction

\( \delta = \frac{4GM}{c^2 R} \)

This is Einstein’s formula for the deflection angle ( \( \delta \) ) of starlight grazing the Sun, where:

Gravitational constant: \( G = 6.674 \times 10^{-11}~\text{m}^3\,\text{kg}^{-1}\,\text{s}^{-2} \\ \)
Mass of the Sun: \( M = 1.989 \times 10^{30}~\text{kg} \\ \)
Speed of light: \( c = 3.00 \times 10^8~\text{m/s}\\ \)
R is the radius/distance from the Sun’s center where the light ray is passing

At the solar limb where R is the same as the Sun’s radius then:

\( R = R_\odot = 6.96 \times 10^8~\text{m} \). Substitute this into the formula like so:

\( \delta = \frac{4GM}{c^2 R_\odot}
= \frac{4 \times (6.674 \times 10^{-11}) \times (1.989 \times 10^{30})}
{(3.00 \times 10^8)^2 \times (6.96 \times 10^8)} \)

\( \delta \approx 8.487 \times 10^{-6} \text{ radians} \), the deflection angle at the Sun’s rim.

And converting radians arcseconds (206265 arcseconds per radian) we get

\( \delta \approx 8.487 \times 10^{-6} \times 206265 \approx 1.75 \) arcseconds

Adjust for 67 Tauri’s apparent distance from the Sun

For 67 Tauri, which lies approximately 1.2–1.5 solar radii (r) from the Sun’s center, the expected deflection is:

\( \delta = \frac{4GM}{c^2 R_\odot} \cdot \frac{R_\odot}{r} \approx \frac{1.75^{”}}{r} \)

\( \delta \approx 1.17^{”} \quad \text{to} \quad 1.46^{”} \)

So, the measured deflection of approximately 2.1 arcseconds is somewhat higher than expected. However, given:

• Image projection distortions
• Inaccuracies in the Stellarium overlay projection
• Sub-pixel centroiding uncertainty
• Manual centroiding for alignment and offset detection

…the result is remarkably close and very much in the spirit of Eddington’s original work.

This small experiment was a fun way to relive one of the greatest moments in science. With a bit of patience and publicly available images, it’s possible to experience Eddington’s achievement for yourself.

---

Angular Separation Calculation

To calculate the angular separation between 65 Tauri and 67 Tauri, use coordinates:

65 Tauri
RA = 04ʰ 25ᵐ 22.1655ˢ = 66.34235°
Dec = +22° 17′ 37.9375″ = +22.29387°

67 Tauri
RA = 04ʰ 25ᵐ 25.0152ˢ = 66.35423°
Dec = +22° 11′ 59.9876″ = +22.19999°

The spherical angular separation formula:

\(\theta = \arccos\left[
\sin(\delta_1)\sin(\delta_2) +
\cos(\delta_1)\cos(\delta_2)\cos(\alpha_1 – \alpha_2)
\right]\)

Substituting the values (converted to radians):

\(\alpha_1 = 1.157892441 \, \text{rad}, \quad \alpha_2 = 1.158099786 \, \text{rad}\)
\(\delta_1 = 0.3891014345 \, \text{rad}, \quad \delta_2 = 0.3874629194 \, \text{rad}\)

\(\theta = \arccos\left[
\sin(0.38910..)\sin(0.38746..) +
\cos(0.38910..)\cos(0.38746..)\cos(1.15789.. – 1.15809..)
\right]\)

\(\theta \approx \arccos(0.9999986392) \approx 0.001649 \, \text{rad}\)

Converting to arcseconds:

\(\theta = 0.0016497 \times \frac{180 \times 3600}{\pi} \approx 340\)

So, the angular separation between 65 Tauri and 67 Tauri is approximately \( \boxed{340~\text{arcseconds}}\).